회귀분석 - 선형회귀 (2)
1. 선형회귀의 사례
1.1 몸무게와 키 상관관계 찾아내기
예시 : 방정식을 배운 머신이는 몸무게와 키의 데이터를 획득했다. 일정하게 증가하는 패턴이 있어서 미리 몸무게를 알면 키를 알 수 있을 것이라고 생각했다.
- 키와 몸무게 간의 데이터
weights = [87,81,82,92,90,61,86,66,69,69]
heights = [187,174,179,192,188,160,179,168,168,174]
- 키와 몸무게 간의 산점도
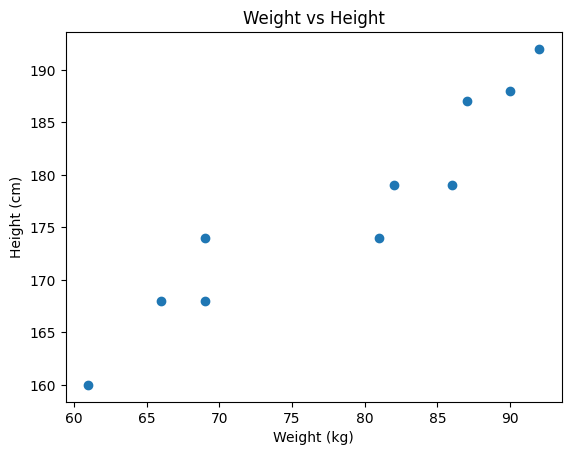
어떤 직선이 현재 데이터를 잘 설명한다고 할 수 있을까?

아무래도 초록색, 파란색 직선보다는 빨간색 그래프가 적절한 것 같다.
1.2 Data Scientific 한 발상
바로 직선과 점의 간의 거리를 계산하는 것이다. 이를 Error 라고 정의하고 최소의 Error인 직선을 그리면 된다고 생각한다면?
방법 1) 실제 데이터 값 - 직선의 예측 값 = Error
- ①번 실제 데이터: 187, 예측 데이터: 187 Error: 0
- ②번 실제 데이터: 174, 예측 데이터: 181 Error: -7
- ③번 실제 데이터: 174, 예측 데이터 : 169 Error: +5
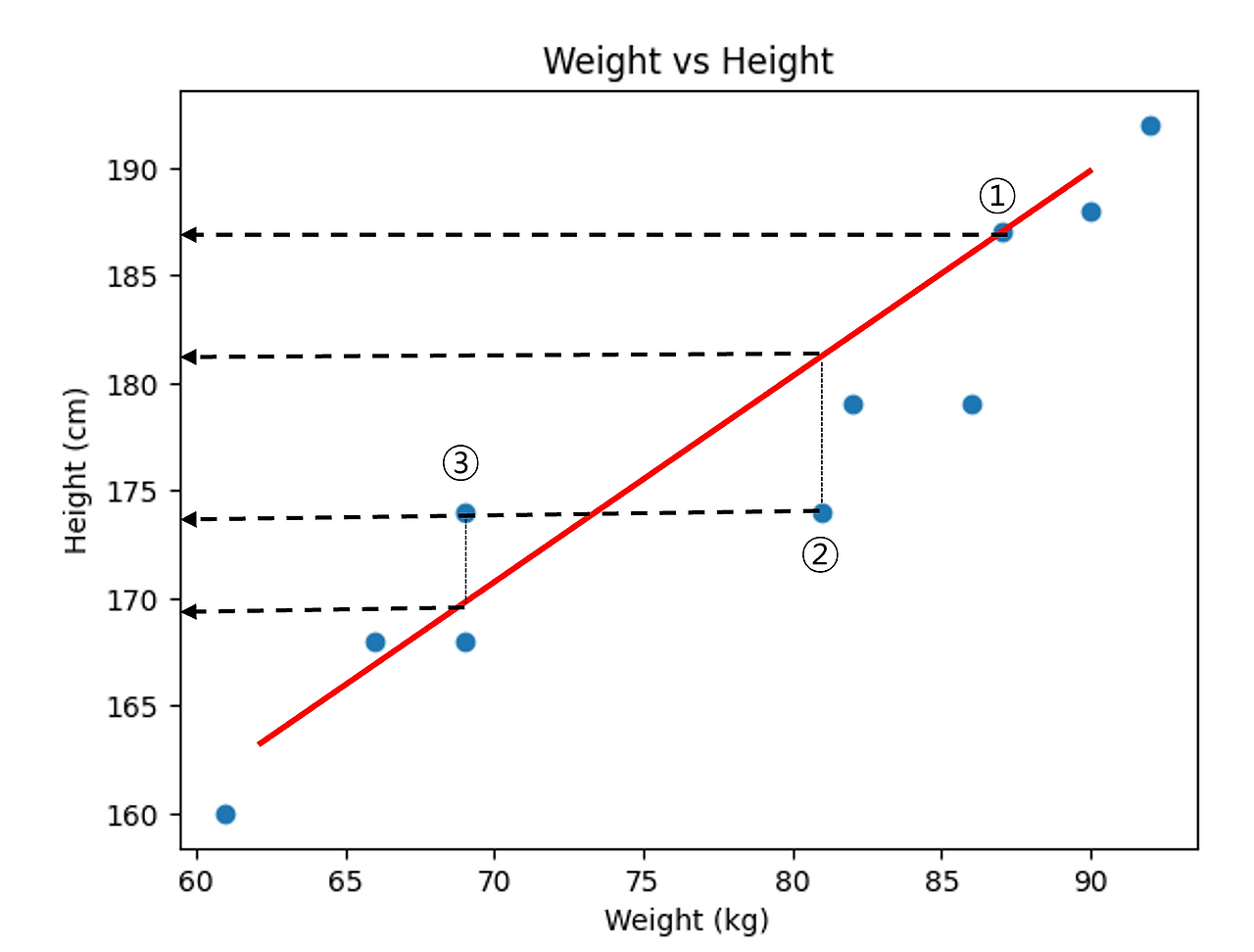
선분을 기준으로 위에 있는 데이터의 거리를 계산하면 양수가 되고, 반대로 아래에 있는 것은 음수가 된다. 이 경우 모든 에러를 합치면 서로 상쇄되는 문제가 있었다. 따라서, 음수를 양수로 만들기 위해 제곱한다면?
방법 2) 각각 Error를 제곱하여 모두 더하기
- ①, ②,③의 제곱 합: 49 +25 = 71

데이터가 더 늘어날 수록(④,⑤) 에러는 자연스럽게 값이 커질 수 밖에 없는 것이다! 그래서 데이터의 갯수로 나누기로 했다. 또한 데이터가 제곱 되어 있던 것을 줄이기 위해 root를 씌운다면?
방법3) 전체 에러 합에 데이터의 갯수로 나누기
- ①, ②,③만 고려한다면 71/3 → 23.7

2. 선형회귀 이론
2.1 선형회귀 용어 정리
통계학과 컴퓨터 공학 두 학문 바탕으로 발전해와서 같은 원리이지만 용어는 살짝 다르다.
만약 몸무게를 알면 키를 알 수 있다고 가정해본다면?
공통
- Y는 종속 / 결과 변수
- X는 독립 / 원인 / 설명 변수
통계학에서 사용하는 선형회귀 식

머신러닝 / 딥러닝에서 사용하는 선형회귀 식

두 수식이 전달하는 의미는 같다. 회귀 계수 혹은 가중치의 값을 알면 X가 주어졌을 때 Y를 알 수 있다.
편의를 위해 X의 계수를 가중치라고 지칭
+ 예시 : 몸무게와 키 데이터를 이용해서 선형회귀 식을 만들면, y = 0.86x + 109.37
이 뜻은, 1kg 증가할때마다 키가 0.86 cm 증가한다는 것으로 해석 할 수 있다.
+ 추가 질문
- Q1) β0 는 1차 방정식의 Y절편에 해당하는 걸 알겠어요. 그런데 ε 은 왜 따로 있는건가요?
- 우리가 몸무게와 키에 대한 선형회귀식을 만들었지만, 해당 식이 모든 데이터를 완벽하게 설명할 수 없어요. 이때 완벽한 설명이란 실제 데이터값 = 예측 데이터 이라고 할 수 있어요. 다시 말해 에러(②,③)의 값을 표현하기 위해서 있는 것 입니다.
- Q2) 가중치 w 를 알게 되면 X값에 대하여 Y값을 예측할 수 있다는 것은 이해가 되는데, 그럼 가중치는 어떻게 구하죠?
- 이런 물음이 들었다면 머신러닝을 관통하는 질문입니다. 데이터가 충분히 있다면 가중치를 “추정”할 수 있습니다. 이는 심화 내용에서 다루도록 할게요! 이 부분은 현재는 그래프를 수도 없이 그려서 에러를 “최소화”하는 직선을 구한다고 생각하시면 됩니다.
3. 회귀분석 평가 지표
3.1 회귀분석의 평가지표
* 회귀 평가지표 - MSE
위 예시의 에러 정의 방법
- 방법1) 에러 = 실제 데이터 - 예측 데이터 로 정의하기
- 방법2) 에러를 제곱하여 모두 양수로 만들기, 다 합치기
- 방법3) 데이터만큼 나누기

y값의 머리에 있는 ^ 표기를 hat 이라고 하며, 예측한 수치에 표기한다.
* Mean Squared Erorr(MSE)

앞으로의 숫자 예측 문제는 어떤 모델을 만들어도 MSE 지표를 최소화하는 방향으로 진행
* 기타 평가 지표
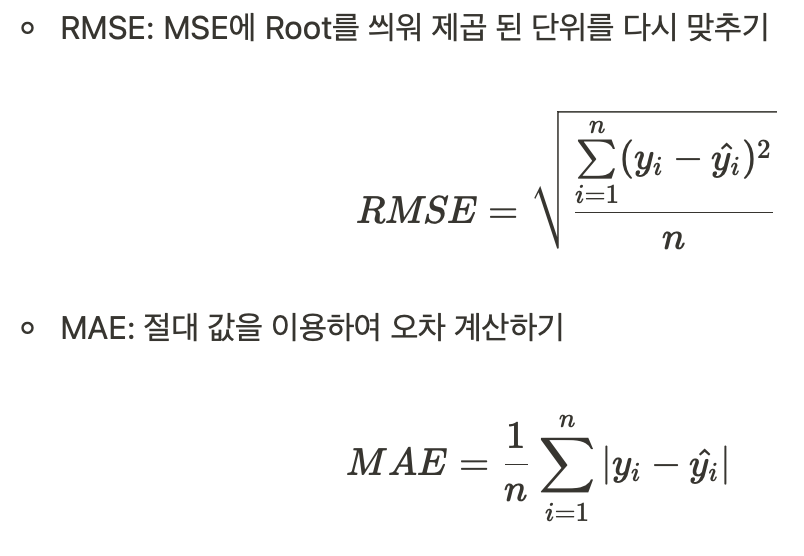
3.2 선형회귀만의 평가 지표 R Square
숫자를 예측하는 회귀분석에서 선형회귀에서만 평가되는 지표가 있다.
R square 는 전체 모형에서 회귀선으로 설명할 수 있는 정도를 뜻함.
- 기초 용어


- R Square의 정의


- 해당 값에 대한 설명력 = 94%
- 단, 모든 데이터에 대해서 위 계산을 수행
4. 선형회귀 적용